Convert 1D Array into 2D Array: You are given a 0-indexed 1-dimensional (1D) integer array original, and two integers, m and n. You are tasked with creating a 2-dimensional (2D) array with m rows and n columns using all the elements from original.

The elements from indices 0 to n - 1 (inclusive) of original should form the first row of the constructed 2D array, the elements from indices n to 2 * n - 1 (inclusive) should form the second row of the constructed 2D array, and so on.

Return an m x n 2D array constructed according to the above procedure, or an empty 2D array if it is impossible.

Example 1:

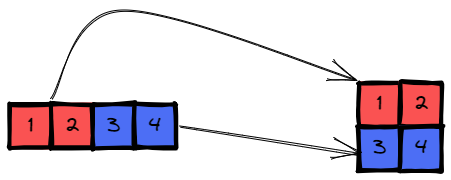
Input: original = [1,2,3,4], m = 2, n = 2
Output: [[1,2],[3,4]]
Explanation: The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, [1,2],
becomes the first row in the constructed 2D array.

The second group of n=2 elements in original, [3,4],
becomes the second row in the constructed 2D array.

Example 2:

Input: original = [1,2,3], m = 1, n = 3
Output: [[1,2,3]]
Explanation: The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.

Example 3:

Input: original = [1,2], m = 1, n = 1
Output: []
Explanation: There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.

Constraints:

• 1 <= original.length <= 5 * 10^4
• 1 <= original[i] <= 10^5
• 1 <= m, n <= 4 * 10^4

Try this Problem on your own or check similar problems:

1. Reshape the Matrix

Solution:

public int[][] construct2DArray(int[] original, int m, int n) {
    if(original.length != m * n) return new int[][] {};
    int[][] result = new int[m][n];

    for(int i = 0; i < original.length; ++i){
        int row = i / n, column = i % n;
        result[row][column] = original[i];
    }

    return result;
}

Time/Space Complexity:

• Time Complexity: O(n)
• Space Complexity: O(1)

Explanation:

We first check if we can construct the 2D array (matrix) by checking if the product of input dimensions m and n is equal to the size of input array. We iterate over input array and calculate each element’s new position in the matrix. We’re doing this by first calculating the row in the matrix by dividing the current index i with number of columns (in other words while i < n the division will result in 0-row, we can fit the the first i elements i < n in the first row, when we get to the element at index 3 in the input array we have to go a level down since we already have 3 elements in the first row). We calculate the column by taking the remainder of the current index i when divided by n (e.g. we know for index 4 in the input array the row in matrix will be 1, and we can get column position by checking the modulo/remainder of division with n, so index 3 will be placed first, index 4 second…).